엔트로피, 크로스 엔트로피
엔트로피: 간단히 말하면, 어떤 정보의 불확실성을 어떠한 "정도"로 나타낸 것인데, 여기서 확률이 아닌 "정도"라고 하는 이유는 얼마든지 0보다 큰 수가 나올 수 있기 때문이다.
이게 애매모호 하다고 생각이 들면, 무언가 발생할 확률, 즉 무언가 발생하는 것을 예측하기 어려우면 어려울수록 엔트로피는 높아진다는 뜻이다.
엔트로피의 값 자체에 의미를 부여하려고 했지만, 실제로 엔트로피는 단순한 수에 불과하다고 마무리가 되었다. 마치 만렙이 얼마나 높은지 모르는 상태의 Lv을 보는 것이라고 할까, Lv 50이라고 봐도, 이게 높은지 낮은지 객관적으로 바라볼 수 없듯이 엔트로피 또한 그렇다.
동전 던지기의 엔트로피는 약 0.693, 6개의 면이 나오는 주사위의 엔트로피 같은 경우에는 약 1.79가 나온다.
기본적으로 엔트로피는 통계의 기대값으로 표현한다, 말그대로 이정도로 예측이 되는 것 같다는 의미이기 때문이다. 하지만 식을 이해하기 위해서는 우선 가정을 잘 생각해야 한다.
우선 정도를 나타내고 싶지만, 이 값이 얼마나 커질지는 아무도 모른다. 따라서 최대한 작은 값으로 나타낼 수 있으면 좋겠다는 것이 시작이고, 이를 모든 사람들이 알아들을 수 있게 표현 하고 싶은게 시작점이다. 그리고 이를 정보이론의 아버지 클라우드 섀넌이 bits(비트)로 나타내면 된다고 하였다. 이를 다른 말로 "정보를 표현하는데 필요한 최소 평균 자원량"이라고 하기도 한다(feat. 혁펜하임)
앞서 내세운 동전과 주사위는 나오는 결과들이 정해져 있다.(동전은 앞뒷면, 주사위는 1~6 숫자 중 하나)
그렇다면, 현실에서 발생하는 일을 예측하는 것은 어떨까?
누가 지각할 확률, 내가 베껴서 낸 숙제/과제가 무사히 통과 될 확률 등, 우리가 계산을 통해서가 아니라 순수한 "감"을 통해서 생각하는 것들을 엔트로피로 표현해보자.
그리고 그 발상을 우선 "발생할 확률이 낮은 일"에 큰 값을 주고 "자주 발생하는 일"에는 작은 값을 준다고 한다. 이에 따라 엔트로피를 "깜짝도"라고 표현하는 곳도 있다("프로그래머를 위한 확률 통계"). 엔트로피를 "깜짝도"라고 표현한다면 엔트로피가 클수록 우리가 깜짝 놀라는 정도가 높아진다는 것이다(아니 이런 일이 발생할 수 가!!).
그래서 "발생 확률이 낮은 값"은 엔트로피가 커야 하므로 어떻게 다시 큰 값으로 나타낼 수 있을까?하는 곳에서 등장하는 것이 log()함수이다.
여기서 다시 "그럼 처음부터 자주 발생하는 일을 큰 값으로 하면 되는거 아닌가?"라는 의문이 들었다. 이유는 bit로 표현하는 이 방식은 "컴퓨터"가 계산하는 것이기에, 큰 숫자가 많이 나타날수록 차지하는 메모리 용량이 많아지므로, 자주 발생하는 녀석들은 작은 값으로 해줘야 한다는 현실적인 문제 때문이다.(그리고 이러한 현실적인 문제는 설명해주는 곳이 많지 않다).
다시 "발생 확률이 낮은 값(엔트로피가 큰 값)"을 어떻게 다시 큰 값으로 나타낼 수 있을까?하는 곳에서 등장하는 것이 log()함수이다.
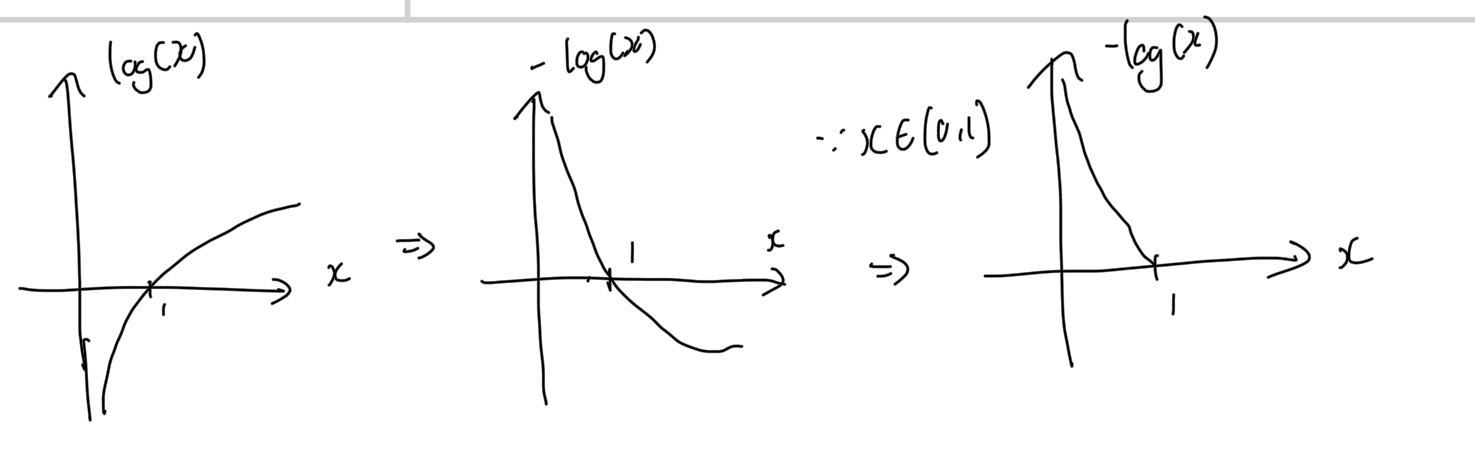
왼쪽 로그 함수에서 출발하면, 마이너스를 취해주면 두번째 그림처럼 뒤집힌다. -> 가장 작았던 값이 제일 커지게 만들어 줄 수 있다.
그리고 "확률"은 0과 1사이의 값을 나타낸다 -> x는 (0,1)범위만 잡아주면 된다, 이러면 무조건 양수(+)가 나타난다.
따라서 각 사건에 대한 엔트로피는 -log(x)라고 할 수 있다.(참고로 이산확률이면 log_2()이고, 연속확률이면 ln()을 취한다)
그리고 이를 기대값을 취해주면

이러한 수식을 얻을 수 있다.
Cross-Entropy: 크로스 엔트로피는 실제 확률 분포를 모르는 상태에서, 이런 확률 분포 아닐까? 하는 예측을 수행하는 것이다.
따라서 실제 확률분포와 내가 예측한 확률분포의 차이가 크로스엔트로피라고 할 수 있다.
다른 말로 크로스엔트로피는 확률 분포를 예측하기 위한 녀석이다. 크로스는 단순히 "실제 분포", "예측 분포" 2개의 분포가 있어서 그렇게 부를 뿐이다.

해당 식에서 q(x)가 실제 분포를 의미하고, p(x)는 예측한 분포를 의미한다 -> 모델이 예측한 분포
기존에 어떤 분포를 따르고 있는 데이터를 모델이 무작위로 "흠... 이런 분포를 따를것 같군"하면서 했을 때 그 값이 크면, 줄여 나가야 한다는 것을 의미한다.
즉, 훈련 데이터를 사용한 예측 모형에서 크로스 엔트로피는 실제 값과 예측값의 차이를 계산하는데 사용할 수 있다는 것이다.
KL-Divergence: 서로 다른 두 분포의 차이를 뜻하는 것이다.

어려워 보이지만, 실제로는 "(크로스 엔트로피) - (엔트로피)"를 나타낸다. 실제 분포에 있는 기대값(엔트로피)은/는 항상 제일 작은 값을 가지므로, KL은 항상 양수를 취할 수 있다.