딥러닝에서 공간을 직관화 하기 위해 어떤 노력들이 있는가?

딥러닝에서 빠질 수 없는 부문 중 하나는 "옵티마이져"다, 한국어로는 "최적화"라고 한다. 

 

다차원 모델의 가장 최적화 되어 있는 지점을 찾기 위해서 온갖 수직을 가져다가 사용하고, 온갖 그림들이 나온다.

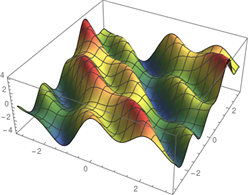
차원이 많으면 많을 수록 사람의 눈으로 파악하기란 불가능하다(애초에 사람은 4차원을 시각적으로 파악하는 것은 불가능하다, 그저 스스로 나름대로의 정의를 내릴 뿐이다)

 

단순 3차원 공간으로도 이렇게 표현하면, 무언가 직관적이지 못하는 경우가 많다. 하지만, 이는 이러한 발상을 심어준다. 이는 물리학에서도 유명한 이론인데 "저차원에서는 해결 불가능 한것이, 고차원에서는 너무나도 쉽게 해결 가능할 수 있다"

 

물리학에서 가장 흔히 드는 비유가 나뭇가지의 그림자이다.

서로 엉켜있고, 보기만 해도 복잡하고, 평면상에서는 하나의 나뭇가지가 다른 나뭇가지를 "관통"한 것처럼 보인다. 하지만 실제 나무는

3차원이기 때문에, 관통하는 것이 아닌 그저 옆으로 지나가는 것일 뿐이라는 것이다. 2차원 관점에서 봤을 때 이상했던 것이 3차원에서는 전혀 이상하지 않는다는 것을 의미한다. 

 

반대로 3차원에서는 이상한 것이 4차원 혹은 그 이상의 차원에서는 전혀 이상하지 않을 수 있다는 것을 의미한다. 

 

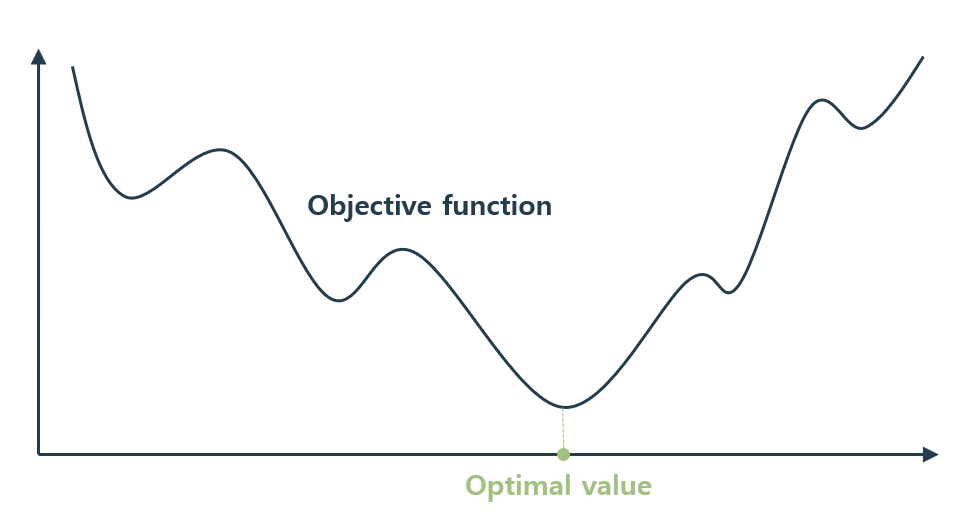
하지만 4차원을 진입하면서, 사람들은 상상을 하기도 힘들어지고, 본인들의 주장을 입증하기 점점 어려워진다. 따라서 사람들은 "최적화 문제" -> 컨벡스(Convex)를 시작하는데, 여기의 주된 사상은 "내가 해결해야 할 문제를 어떻게든 2차원 함수로 만들면, 최적화 할 수 있다"라는 마인드가 있다. 

 

위의 그림은 2차원 평면에 그려져 있지만, 2차 함수라고 착각해서는 안된다. 2차 함수는 y=x^2같은 함수를 의미한다(컨벡스는 원래 "볼록한"이라는 뜻이다).

하지만 저런 다차원 함수를 위 그림처럼 함수가 2차원이 되면, 우리는 미분이 0이 되는 지점이 하나밖에 없다는 것을 알게된다. 이 마인드가 머릿속에 장착되어야 한다. 그래야 옵티마이져 계산식, 혹은 오차함수등 여러가지 이론들을 보면서, "왜 저렇게 하려고 하는지" 이해를 할 수 있었다. 그 전까지는 그저 "아 저 사람이 이렇게 하라고 했으니까, 이렇게 해야지"라고 생각을 하는 것일 뿐이다.