(이산분포-3)기하분포

기하 분포의 정의는 "n번의(n은 우리가 정하는 것이다) 베르누이 시행에서 처음 성공이 나올 때까지 시행한 횟수"이다.

 

기하 분포에는 2가지 정의가 있다. (무엇을 확률 변수로 둘 것인지에 따라 나뉜다)

1. 처음 성공이 나올 때까지 시행한 횟수를 확률 변수로 하는 분포(이 글은 이것을 기준으로 할 것이다)

2. 처음 성공이 나올 때까지 "실패"한 횟수를 확률 변수로 하는 분포

 

예시는 다음과 같다: 한 남여가 연애에서 결혼까지 갈 확률이 5%라고 하면, x번째 사귄 이성과 결혼하게 될 확률분포 p(x)는?

 

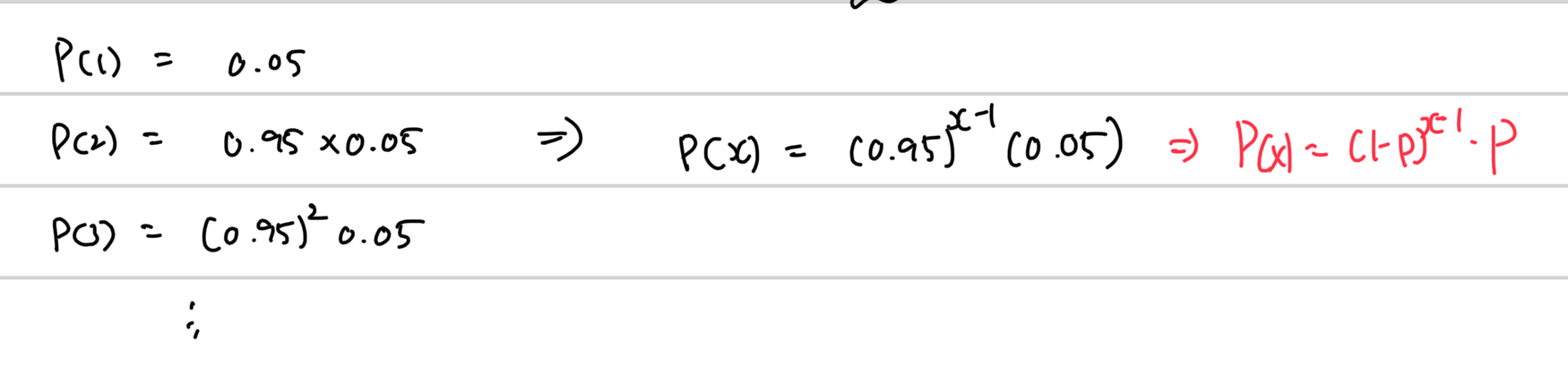
p(1)은 첫번째 이성과 결혼할 확률이고 p(2)는 2번째 이성과 결혼할 확률을 나타내므로, 위와 같은 식을 얻을 수 있다.

 

그리고 기하분포는 다음과 같이 표시한다.

 

그리고 해당 평균과 분산의 유도식은 직접해보는 것이 좋고, 나의 필기 또한 지저분 하기에 여기에는 담지 않는 대신, 중간에 "로피탈 정리"라는 개념이 나오고, 이를 설명을 해주시지는 않기 때문에 이 로피탈 정리에 대해 설명하겠다.

 

이런식으로 둘다 극한을 취했을 때 0이 나오거나 무한이 나올경우, 더 정확히는 

이런식으로 극한 값이 판단이 되지 않을 경우 사용되는 것이 "로피탈 정리"이다. 

 

로피탈 정리는 다음과 같다.

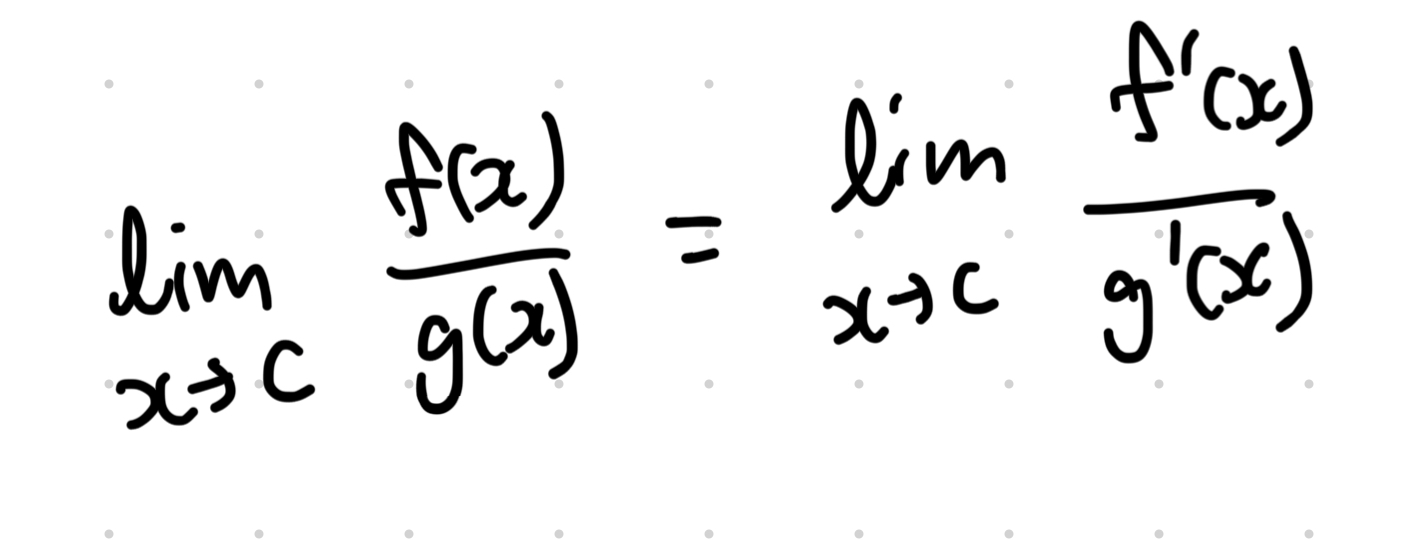
분모 분자에 미분을 취해주고, 극한을 다시 해주는 것과 동일한 결과를 얻는 다는 것이다. 증명은 저도 잘.. ㅎㅎ;;

 

아무튼 기대값(평균)을 구할 때 이런 부분이 나온다.

이 n*(1-p)^n에 극한을 취할 때 이 로피탈 정리에 의해서 0이 된다고 말만 할 뿐 설명은 없기에, 여기서 정리하려고 한다. 

 

다음과 같이 계산된다.

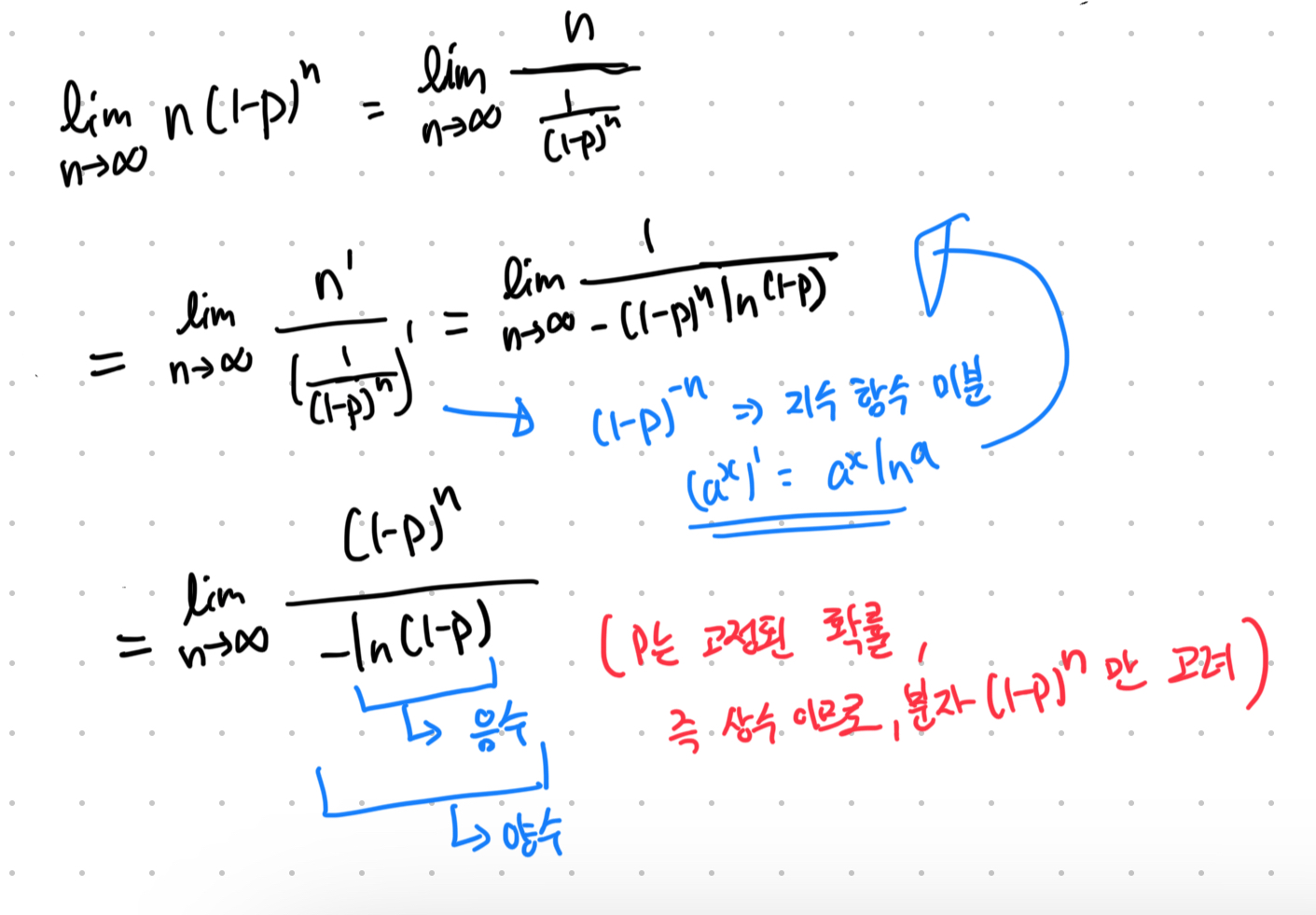
그리고 여기서 (1-p)^n을 함수 그래프로 보면 다음과 같다.

 

따라서 lim{ n*(1-p)^2 } = 0 이 성립되는 것이다.