(간단한 코드)리트코드 704. Binary Search

 

이 문제는 리스트 안에 특정 값을 찾는 문제이고, 답은 생각보다 훨씬 쉽게 찾을 수 있지만, 문제는 binary search 방법으로 해답을 찾는 것을 요구한다.

 

여기서 "바이너리 서치"란 무엇일까?

이런 그림을 많이들 봤을 것이다. 이를 binary tree라고 하며, 항상 "두 가지 선택지에서 하나를 택한다"라는 조건이 있는 상황을 의미한다.

 

(참고로 binary는 0과 1로 판단을 내리는 컴퓨터공학에서 나온 용어이다)

 

이 구조의 특징은 다음과 같다.

여기 나오는 빨간색 점이, 백화점이나 지하철 같은 곳에서 지도를 볼 때, "현 위치"를 나타낸다고 하자. 해당 그림은 1번을 택해서 왼쪽을 가는 그림을 나타낸다.

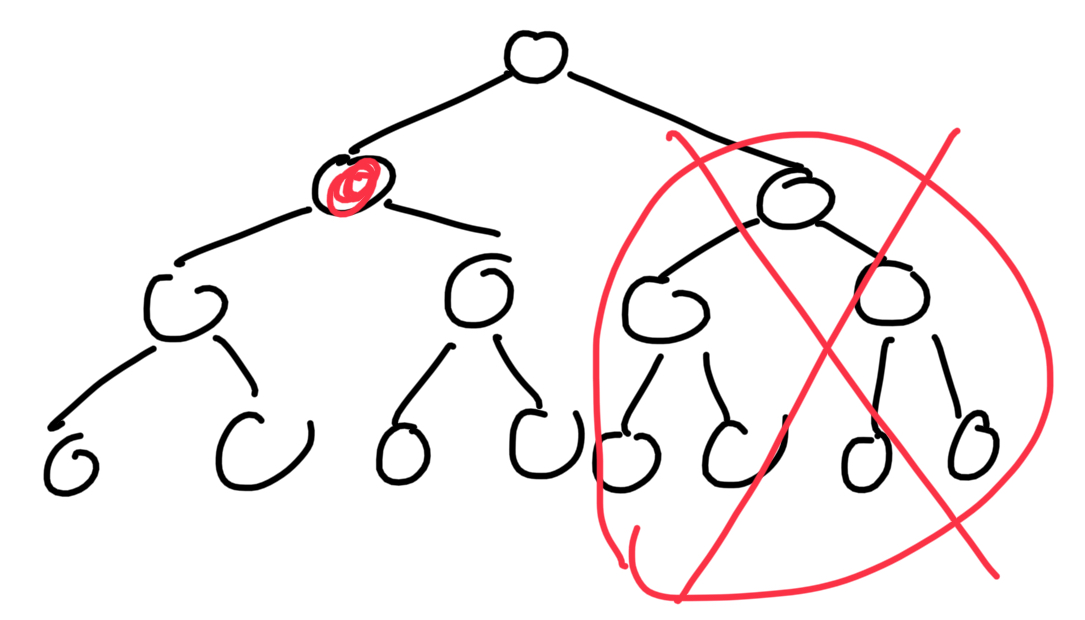
그렇다면, 현 위치가 당연히 바뀔 것이고, 이에 따라 선택하지 않았던 오른쪽은 영원히 볼 수 없을 것이다.

이 뜻은 "선택을 한번 함에 따라, 선택지가 2배 줄어드는 것을 의미한다"

이를 log(n) 시간 복잡도라고 부른다. 왜 log(n) 시간 복잡도라는 하는지는 "로그가 의미하는 것이 무엇인지"에 대해 유튜브에 훨씬 잘 설명하는 사람들이 넘쳐난다.

한번 더 선택을 내린다면, 다음에도 선택지가 2배 줄어드는 현상을 볼 수 있다. 

 

이를 코드로 구현하기 위해서는 two pointer과 같은, "시작"과 "끝"을 나타내는 숫자와 "중간"을 나타내는 값을 사용한다.

코드는 다음과 같다

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        l, r = 0, len(nums)-1
		#시작을 나타내는 l, 끝을 나타내는 r
        while l <= r: #투 포인터의 while문의 조건으로 l<r 혹은 l<=r로 두는 경우가 일반적이다
            mid = (l+r)//2 #중간을 나타내는 mid, 계속 새로운 값으로 갱신해야 하니 while문 안에 위치
            if nums[mid] == target: #만약에 찾고자 하는 값이 mid이라면 답을 내보내고
                return mid
            elif nums[mid] > target: #찾고자 하는 값보다 크면 범위를 l~mid-1로 줄인다
                r = mid - 1
            else: #찾고자 하는 값보다 작으면 범위를 m+1~r로 줄인다.
                l = mid + 1
        return -1 #while문이 끝날 때까지 값이 없다면 -1을 반환한다.

여기서 mid는 middle의 약자로 자주 쓰인다.