1)이항분포는 "베르누이 시행을 여러번 한 것"이라고 한다, 그리고 각 시행은 독립적이다 -> 앞에 어떤 결과가 나왔든 다음 시행에 아무런 영향을 끼치지 않는다는 것이다.
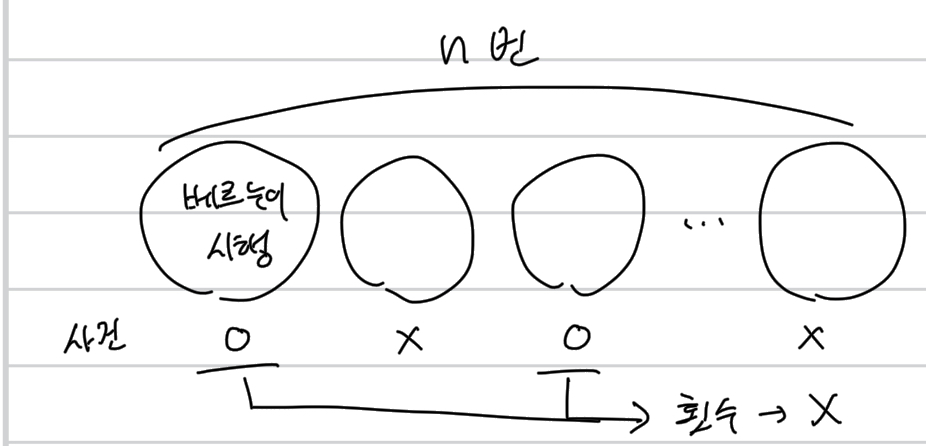
이항분포는 다음 그림처럼 n번을 시행하고(각 시행의 성공 확률을 p라고 한다), 그중에서 몇번을 성공했는지(혹은 실패했는지)를 확률 변수로 둔다.
유튜브 "통계의 본질" 채널에서는 농구선수의 예시를 들었다.
예) 한 농구 선수의 자유튜 성공 확률은 80%라고 하자, 그렇다면 성공확률을 0.8, 실패를 0.2라는 것을 알 수 있다.
10번의 기회에서 자유투 성공 횟수를 X라고 두고, X라는 횟수만큼 성공할 확률을 P(X)라고 본다(통계를 처음 접하는 사람들은 여기서 부터 잘 놓친다) -> 우리는 농구선수에게 10번의 시도를 해보라고 제안하는 것이 아닌, 그저 성공확률 80%만 가지고 예측을 해보는 것이다.

여기서 2번째 줄을 보면, 앞에 숫자 10이 곱해져 있다, 이는 1번의 성공이 몇번째 성공인지에 따라 나뉘기 때문에 그렇다. 비전공자는 이 개념에서 또 순열이랑 헷갈리는 사람들도 많다, "어라 몇번째인지 중요하면 조합이 아니라 순열 아닌가?"라면서 말이다.
경우의 수를 생각하는 관점에서는 조합과 순열이 비슷해 보이지만, 순열은 모든 변수에 의미가 있는 경우 사용하고, 조합은 특정 변수에만 의미가 있는 경우라고 생각해보자(자신만의 해석은 오해를 불러 일으킬 수 있지만, 이마저도 없이 넘어가면 나중에 포기할 수 도 있다). 그리고 확률 변수라는 것이 존재하는 이상, 순열이 나오는 일은 없을 것이다(아마도?).

경우의 수를 나열을 하다보면, 다음과 같은 형상을 띄고, 규칙성을 찾게 된다. 이를 변수로 변환 시키면 다음과 같다.

이러한 공식이 이항분포 함수이다.

순열과 조합 이야기가 나온 김에 공식은 적어두는게 좋겠다(왜 저렇게 나오는 거지?라는 것이 궁금해서 초반에는 유도식을 외우듯이 썻지만, 그냥 공식을 외우게 되었다).
이항 분포 함수는 다음과 같다, X ~ B(n, p): 확률변수 X는 Binomial(이항 분포)를 따른다(앞에 있는 물결표 "~"가 따른다는 의미다), 시행 횟수는 n번이고, 발생확률은 p이다(-> 여기서 p는 각 시행 할 때마다 성공할 확률, 베르누이 시행을 의미하는 것을 잊으면 안된다)
2)평균과 분산: E(X), V(X)
평균이라고 불리기도 하고, 기대값이라고 불리기도 하는 E(X)는 다음과 같다.

여기 있는 P(X)는 베르누이 시행의 확률을 의미하는 것이 아니라, x번 성공할 확률의 확률 분포 함수를 의미한다(바로 위에 P(x)=nCx * p^x * (1-p)^(n-x) 라고 파란색 글자로 적은것을 의미한다).
여기까지가 혼자 책을 보면서 자주 헷갈렸던 부분들이었다. 분산 같은 경우는 결국 평균을 사용해 구하는 것이므로 크게 헷갈리게 없었다.
E(X) = n*p, V(X)=n*p*(1-p)=n*p*q 라는 것을 알 수 있는데, 이 과정은 정말로 손으로 풀어보는 것이 좋다.
https://www.youtube.com/watch?v=EWlz_FX5icM&list=PLmljWRabIwWDCLjAMfTPigyTe-jtsLca1&index=5
'(딥러닝을 위한)확률과 통계 > 다양한 확률 분포' 카테고리의 다른 글
| (이산분포-6) 초기하 분포 (0) | 2024.11.23 |
|---|---|
| (이산분포-5) 푸아송 분포 (1) | 2024.11.22 |
| (이산분포-4)음이항 분포 (3) | 2024.11.21 |
| (이산분포-3)기하분포 (0) | 2024.11.20 |
| (이산분포-1)베르누이 분포 (1) | 2024.11.18 |