딥러닝 성장일지

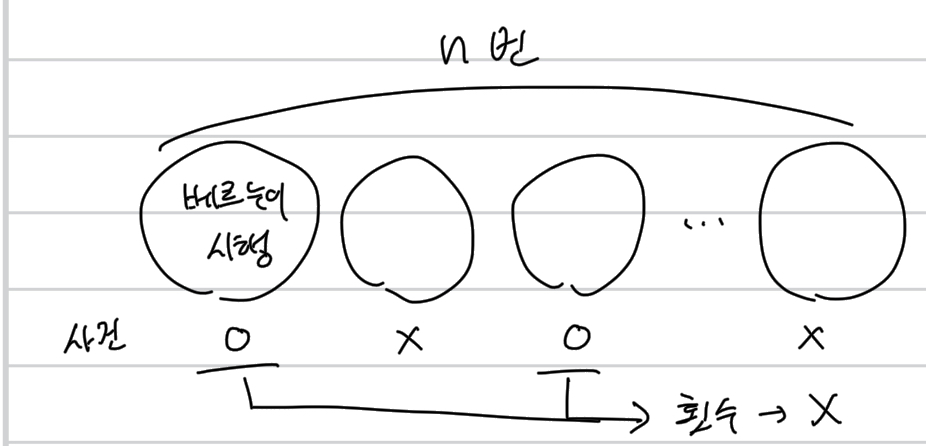
기하 분포의 정의는 "n번의(n은 우리가 정하는 것이다) 베르누이 시행에서 처음 성공이 나올 때까지 시행한 횟수"이다. 기하 분포에는 2가지 정의가 있다. (무엇을 확률 변수로 둘 것인지에 따라 나뉜다)1. 처음 성공이 나올 때까지 시행한 횟수를 확률 변수로 하는 분포(이 글은 이것을 기준으로 할 것이다)2. 처음 성공이 나올 때까지 "실패"한 횟수를 확률 변수로 하는 분포 예시는 다음과 같다: 한 남여가 연애에서 결혼까지 갈 확률이 5%라고 하면, x번째 사귄 이성과 결혼하게 될 확률분포 p(x)는? p(1)은 첫번째 이성과 결혼할 확률이고 p(2)는 2번째 이성과 결혼할 확률을 나타내므로, 위와 같은 식을 얻을 수 있다. 그리고 기하분포는 다음과 같이 표시한다. 그리고 해당 평균과 분산의 유도식은 직..

1)이항분포는 "베르누이 시행을 여러번 한 것"이라고 한다, 그리고 각 시행은 독립적이다 -> 앞에 어떤 결과가 나왔든 다음 시행에 아무런 영향을 끼치지 않는다는 것이다. 이항분포는 다음 그림처럼 n번을 시행하고(각 시행의 성공 확률을 p라고 한다), 그중에서 몇번을 성공했는지(혹은 실패했는지)를 확률 변수로 둔다. 유튜브 "통계의 본질" 채널에서는 농구선수의 예시를 들었다.예) 한 농구 선수의 자유튜 성공 확률은 80%라고 하자, 그렇다면 성공확률을 0.8, 실패를 0.2라는 것을 알 수 있다.10번의 기회에서 자유투 성공 횟수를 X라고 두고, X라는 횟수만큼 성공할 확률을 P(X)라고 본다(통계를 처음 접하는 사람들은 여기서 부터 잘 놓친다) -> 우리는 농구선수에게 10번의 시도를 해보라고 제안하는..

지겹게도 듣게 되는 분포 중에 하나이다. 정의도 간단하다, "일어나냐" "안 일어나냐" 2가지 상황만 있으며, 발생할 확률을 의미한다. 예도 흔한 이야기들이다(동전 던지기, 주사위에서 짝수냐 홀수냐 등)왜 매번 이녀석이 항상 나오는 것일까? 이유는 간단하다, 이산분포는 거의 모두 베르누이를 통해 형성된 새로운 가능성이기 때문이다. 그래서 베르누이 분포가 아닌 베르누이 시행이라고 더 많이 말한다. 딥러닝에서는 이론적이 부문에서 베르누이를 자주 볼 수 있지만, 점점 잘 안보인다, 근데 없는게 아니라 항상 존재하기 때문에 그만큼 중요하다 이렇게 설명하면, 보통 초창기에 "제대로 하고 넘어가야지!"라고 하지만, 의미가 없었다, 결국은 다른 분포를 공부하면서 자연스럽게 외워졌다,하지만 다른 분포가 뭔가 잘 이해가..